运筹学一维搜索算法编程实践报告

2021-10-21

字数统计: 1.5k字 | 阅读时长: 5分

1. 实际问题

设有N个人要进行检测排查，该人群患病率为P。假设每组混采样本数为k，若检测为阳性，则对该组样本再逐一检测。试用一维搜索的方法求使得总检验次数最少的k。

2. 分析

每组检测次数为随机变量 X分布律为：

在这里插入图片描述
每组检测次数的期望：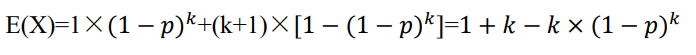

N/k组检测次数的期望：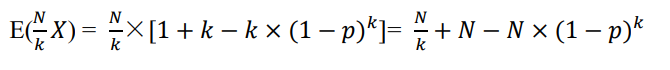

3.编程

3.1 确定搜索区间

假设检测的总人数有二十万人，患病率千分之一，要求最后得出解的区间长度小于ε=0.001。此时画出每组人数与总检测次数的函数图像如下(k取1~100)，可以定性地看出存在峰值，有最少的检测次数。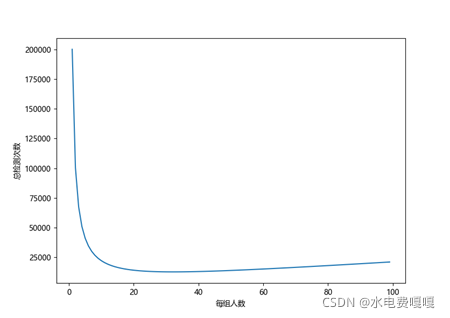
在这里插入图片描述
列出1至100范围内整数值，找到了最小值区间为[31,33]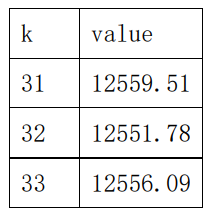

3.2 0.618法

本次编程采用 0.618 法搜索最小值，0.618 法属于一维搜索的序贯试验法，在搜索区间[a, b]内选取两个点𝜆1 < 𝜆2，计算比较 f(𝜆1)、f(𝜆2)函数值，如果f(𝜆1)>f(𝜆2),舍弃区间[a, 𝜆1], 使[𝜆1, b]作为新的搜索区间继续在其中选取两个点；f(𝜆1)<f(𝜆2),则舍弃区间[𝜆2, b]，使[a, 𝜆2]作为新的搜索区间继续在其中选取两个点。
简单来说，使函数值 f(λ)较大的λ称为劣点，每次舍弃的是劣点外侧的区间。
0.618 法迭代步骤如下：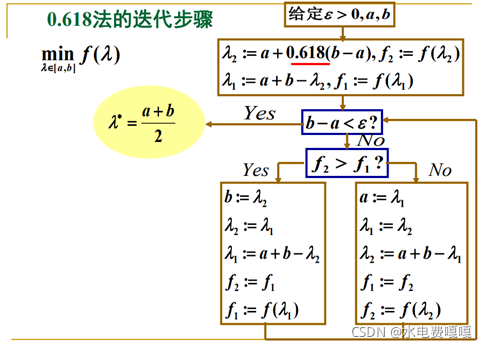
在这里插入图片描述

3.3 0.618法存在的问题

在实际编程中发现，采用 0.618 法，迭代次数过多时，选取的中间两个λ值会远远偏离黄金分割的位置，导致𝜆1 > 𝜆2，在舍弃区间时可能会丢失最优值区间。在不失一般性的情况下，下面以[0,1]区间搜索最小值为例，每次迭代舍去最右边的区间，随着迭代的增多，各个值变化如下。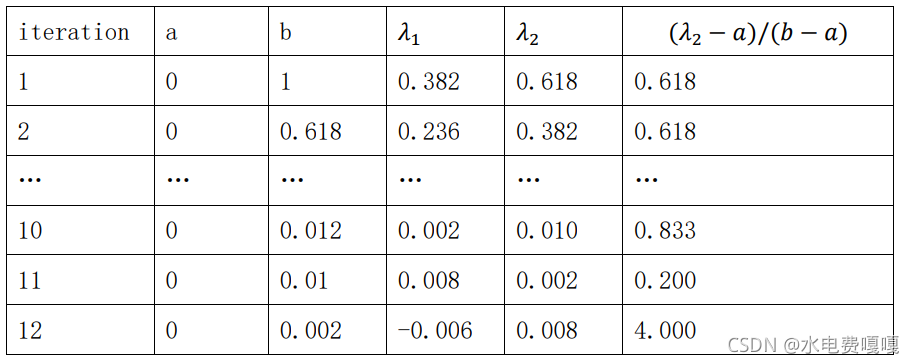
在这里插入图片描述
从上表中可以发现，当迭代到第 10 次时，(𝜆2 − 𝑎)/(𝑏 − 𝑎)值已经严重偏离了 0.618，从而在下次的迭代中导致𝜆1 > 𝜆2，当最优值处于区间(𝜆2, 𝜆1)时，在舍去区间时，会丢失掉最优值所在的区间。

3.4 算法改进

为了避免(𝜆2 − 𝑎)/(𝑏 − 𝑎)过早地偏离黄金分割值，从而导致𝜆1 > 𝜆2，在编程中用(√5 − 1)/2 代替 0.618，重复上述的实验过程，有如下结果。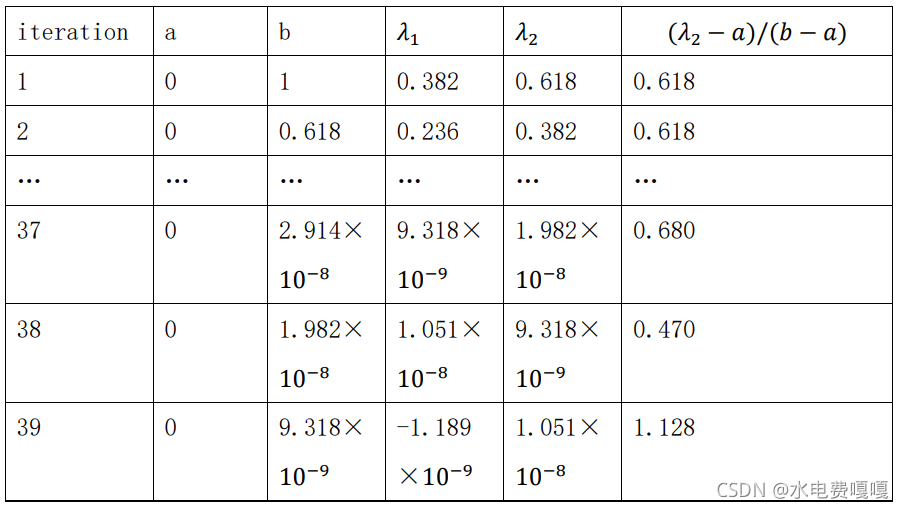
在这里插入图片描述
由于计算机存储位数有限，并不能精确表示(√5 − 1)/2 的值，当迭代次数达到 37 次时，仍会出现(𝜆2 − 𝑎)/(𝑏 − 𝑎)偏离黄金分割值现象，但是与之前迭代 10次相比，迭代次数提高了不少。

3.5 迭代次数计算

本问题初始搜索区间(a, b)为(31, 33),区间长度为 2，每次迭代后区间长度大约缩减为原来的 0.618，最后要求区间长度小于ε=0.001。设经过 i 次后，区间满足精度要求，得到如下不等式：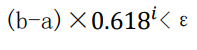
在这里插入图片描述
解不等式得：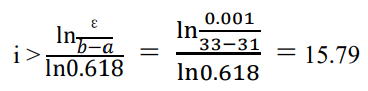

即需要迭代 16 次才能满足精度要求停止。16 次在 37 次之内，不会出现(𝜆2 −𝑎)/(𝑏 − 𝑎)偏离黄金分割值现象，计算过程中不会丢失最优解。

3.6 代码

import math

N = 200000 # 核酸检测人数
p = 0.001 # 患病率

# 总检测次数期望公式
def function_k(k):
    result = N / k + N - N * (1 - p) ** k
    return result

# 搜索最小值
def search_min_k():
    # 搜索区间
    a = 31
    b = 33
    epsilon = 0.001 # 精度
    lambda_right = a + (math.sqrt(5) - 1) / 2 * (b - a) # λ2
    lambda_right_function_value = function_k(lambda_right) # f(λ2)
    lambda_left = a + b - lambda_right # λ1
    lambda_left_function_value = function_k(lambda_left) # f(λ1)
    # 当区间长度小于给出的精度时停止迭代
    while b - a >= epsilon:
        # 当λ2处函数值较大时，舍弃右侧小区间
        if lambda_right_function_value > lambda_left_function_value:
            b = lambda_right # 上一步的λ2作为新的区间右侧端点
            lambda_right = lambda_left # 上一步的λ1作为新的λ2
            lambda_left = a + b - lambda_right # 根据λ到区间端点距离相同的对称性质计算新的λ1
            lambda_right_function_value = lambda_left_function_value # 上一步的λ1处函数值作为新的λ2处函数值
            lambda_left_function_value = function_k(lambda_left) # 计算新的λ1函数值
        # λ1处函数值较大或相等时，舍弃左侧小区间
        else:
            a = lambda_left # 上一步的λ1作为新的区间左侧端点
            lambda_left = lambda_right # 上一步的λ2作为新的λ1
            lambda_right = b - (lambda_left - a) # 根据λ到区间端点距离相同的对称性质计算新的λ1
            lambda_left_function_value = lambda_right_function_value # 上一步的λ2处函数值作为新的λ1处函数值
            lambda_right_function_value = function_k(lambda_right) # 计算新的λ2函数值
    return (a + b) / 2

min_k = search_min_k()
print(f'min_k={min_k} function_value={function_k(min_k)}')

4. 运行结果与结论

程序运行的结果为min_k=32.12709,function_value=12551.68863，即检测总人数为二十万，患病率为千分之一，精度值为0.001时，每组混采样本数k=32.12709时，总检测次数最少，为12551.68863次。由于精度值为0.001，精确的k值在[32.12709-0.0005, 32.12709+0.0005]区间。

当患病率为千分之一时，计算得到的使总检测次数最少的每组混采样本数k约为32。而全国新冠肺炎的患病率远小于千分之一，理论上来说每组混采样本数k应该更大，但是实际做新冠肺炎核酸检测时，每组混采样本数k多为5或10，可能有其他实际因素的考虑。

直接使用0.618作为选取λ比值时，随着迭代次数的增多，当迭代到第10次时，(λ2-a)/(b-a)值会偏离0.618，从而导致λ1>λ2，当最优值处于区间(λ2,λ1)时，在舍去区间时，会丢失掉最优值所在的区间。在实际编程中使用(√5-1)/2代替0.618，延后了比值偏离迭代失败出现的时机。